It's a bit of a cliche that the best papers are the ones that raise more questions than they answer (in fact, many papers seem to answer hardly anything at all on close inspection and it doesn't mean they're great). But I think this might be one of those papers for which the cliche holds true in a positive sense. Rigotti and colleagues (2013, Nature) reported a really intriguing re-analysis of some single-unit data from macaque PFC. The central idea here is to attempt to estimate the dimensionality of the neuronal representation, and to connect this to task performance. This sounds abstract, but I think the strength of the paper lies in how the authors frame dimensionality in terms of linear separability.
The basic idea goes like this: If we represent neuronal firing rates in some task with a n by c matrix where n represents cells and c the unique conditions, the most task-related dimensions that a neural representation can encode would equal to c. Ordinarily, you could take the rank of the matrix (assuming n=>c) to test how many dimensions are present. The rank will be less than c if some of the conditions are linear combinations of each other. The catch is that neuroscientific data is noisy, which inflates the dimensionality all the way up to n in practically all cases. So how do you estimate the dimensionality in the presence of noise?
Rigotti's solution is to approach the problem indirectly via linear separability. One way to think of a representation's dimensionality is that it's related to the number of ways in which you can bisect the space with a discriminant. Imagine arbitrarily splitting the conditions into two classes, and using a standard linear discriminant analysis to find a hyperplane that separates the two classes. If the matrix is full rank, this is always possible for all arbitrary splits of the conditions. So the number of successful discriminants (there's 2^c) is related to the rank of the matrix. This is useful because we can now deal with the noise by cross-validating the discriminant. So the number of successful cross-validated discriminants (and by successful, we mean accuracy over some threshold) provides a noise-corrected measure of the dimensionality of the underlying representation.
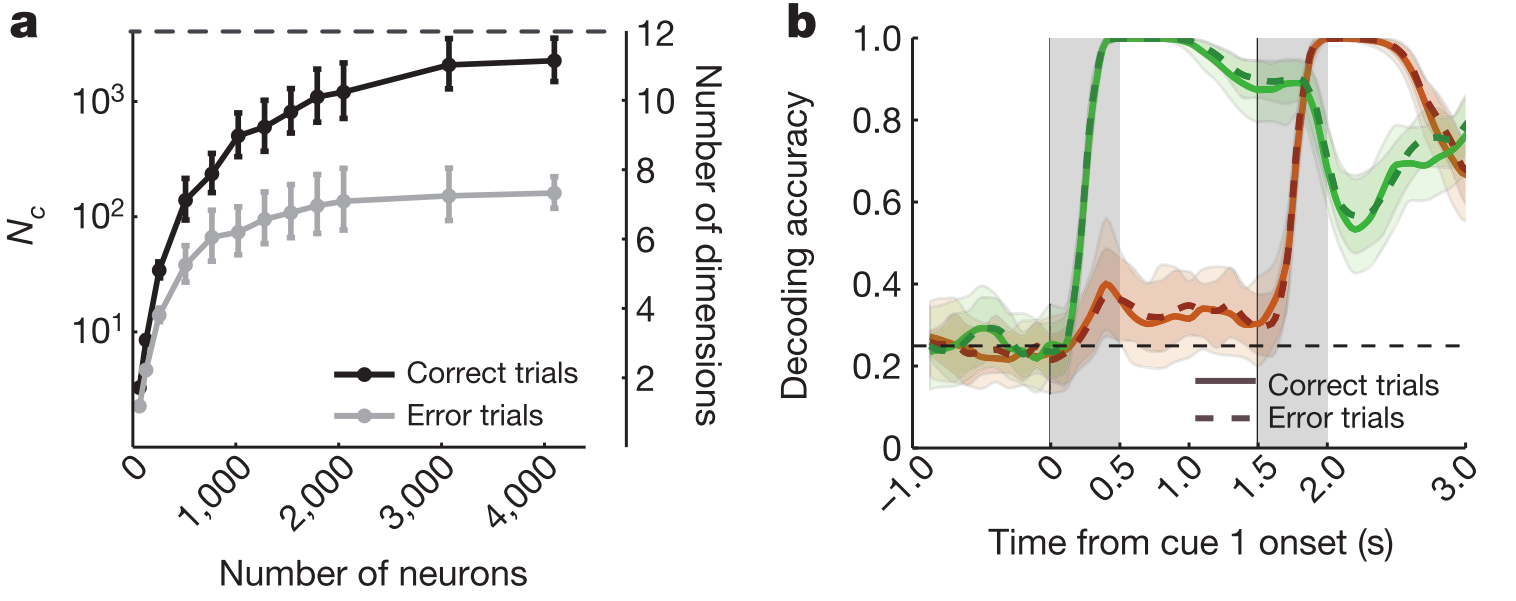
The most convincing evidence in the paper is in Fig 5, of which two panels appear below. (a) shows that the estimated dimensionality is lower for correct trials than for error trials. By contrast, decoding of the stimulus cue is similar for these trial types (b), which makes two points: first that it's not that the monkey simply fell asleep on the error trials because this stimulus distinction is present in the responses. Second, and less intuitively, this one arguably task-relevant dimension does not distinguish correct and error trials, while the total count over many discriminants does, even though a good number of these splits would have very little behavioural relevance. This is puzzling.
A final few notes on this:
- The paper has a strong spin on the topic of 'non-linear mixed selectivity', by which the authors simply mean that a neuronal code based on tuning to single dimensions or linear combinations thereof cannot support the kind of high dimensionality they observe here. Lots of analyses in the paper focus on removing linear selectivity and characterising it separately in different ways to support the case that non-linear tunings are essential for this. I don't think this point is as new or as controversial as it is presented in the manuscript.
- The authors' dimensionality estimation approach is neat for this application because it has a natural link to neuronal readout - part of the popularity of linear classifiers stems from the intuitive cartoon of the weights vector as the synaptic weights on some downstream representation. In this sense, a higher-dimensional representation seems more suited to flexible behaviour because a downstream region would be able to make a large number of distinctions by changing the weights. But there are of course many other ways to estimate the rank of noisy data and one wonders how this approach compares to methods used in other fields, where the classifier intuition is less appealing but the problem potentially very similar.
- If PFC really furnishes such high-dimensional representations (note that all stimulus dimensions are present in the population code according to Fig 5A above), why are some distinctions behaviourally more difficult than others? Presumably monkeys would find it much harder to learn an XOR-like stimulus-response mapping than a simple feature mapping, which doesn't seem to follow if the code were this high-dimensional.
Reference
Rigotti, M., Barak, O., Warden, M. R., Wang, X.-J., Daw, N. D., Miller, E. K., & Fusi, S. (2013). The importance of mixed selectivity in complex cognitive tasks. Nature, 497(7451), 585–90. http://doi.org/10.1038/nature12160.
Comments
comments powered by Disqus